[알고리즘]Heap sort 그리고 조금의 merge sort &Quick sort
Merge Sort Revisited
: 잘게 쪼개서 합치면서 비교하며 정렬

worst case time complexity = n lg n + n + 1
-> 합치는 과정에서 2개 이상을 한 번에 처리할 수 있기 때문에 아까보다 좋아짐!
- 더욱 개선 할 수 있는 방법?
1. Dynamic programming
2. LInked list
3. More complex merge algorithm
merge sort의 자세한 알고리즘은 요기...
[알고리즘] Binary Search, Mergesort(DIvide and Conquer)
DIvide and Conquer Approach - Divide : 인스턴스가 너무 커서 계산이 힘들다면 작게 쪼개서 계산한다. - Conquer : 작아진 인스턴스를 해결한다. - Combine : 해결한 인스턴스를 재조립한다. -> Top-down approach(하
meongjeong.tistory.com
Quick Sort Revisited
Time complexity

- merge sort보다 엄청 나쁘지는 않음..?
- 하지만 in-place sort가 아님
-> space complexity가 나쁨!
-> extra space를 줄이자! ~> 노력하면 worst case가 Θ(lg n)까지 줄일 수 있음!
Heap Sort

MS< QS랑 다르게 in-place sorting algorithm(제자리 정렬 알고리즘)
- worst case time complexity : Θ(n lg n) Complete binary tree- 모든 internal node(일반적인 노드)는 모두 2개의 자식 노드를 갖는다.- 모든 leaf node(마지막 노드)는 모두 같은 깊이에 존재한다 (모두 depth of d)Essentially CBT(조금 부족한 바이너리트리..?)- d - 1까지는 complete binary tree- 깊이 d에 있는 노드들은 왼쪽부터 채워나간다 (아직 노드들이 생겨나는중...?)Heap
-> 부모노드는 무조건 자식노드보다 큰 값을 갖고 있다.
The array representation of the heap
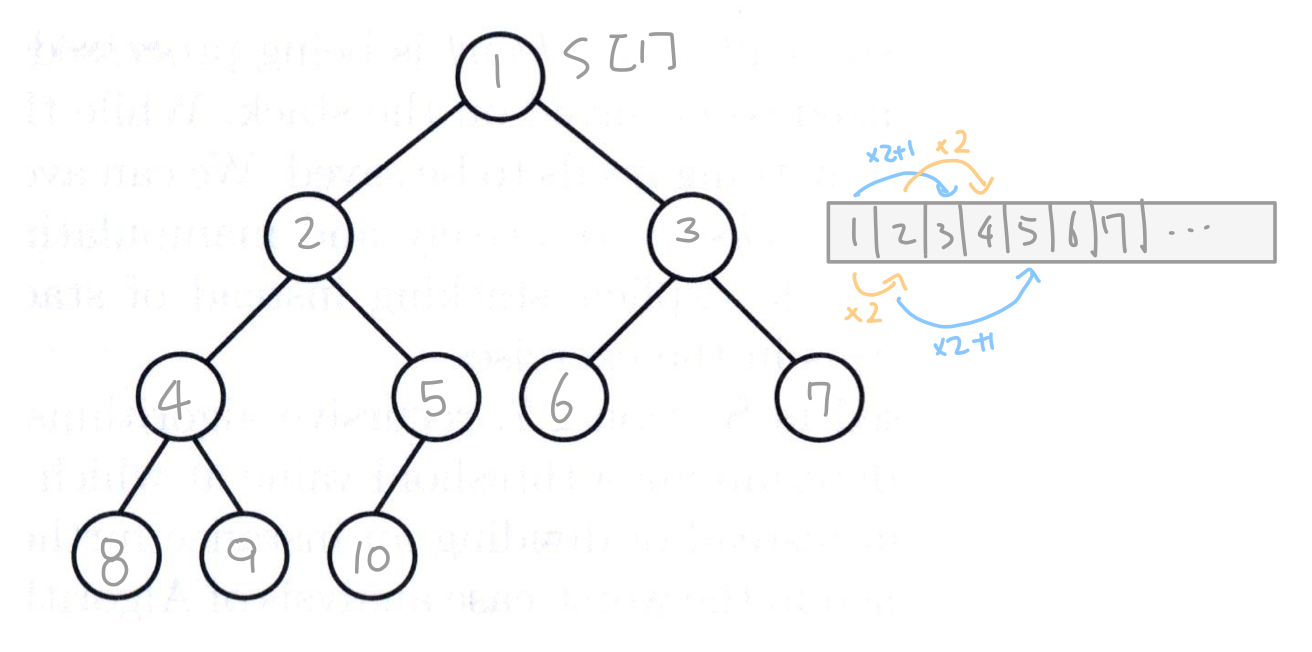

heap은 바이너리 트리이기 때문에 자식 노드의 위치를 구할 수 있다.
left node = parent * 2
right node = parent * 2 + 1
그래서 아무튼 정렬하는 방법

-> root 노드가 가장 큰 값이니까 그걸 사용하면 되는거 아닐까요?
Q. 그럼 그 비어있는 root 자리는?
A. 마지막 노드 가져오기!
Q. 그럼 트리가 고장나지 않을까요?
A. 그럼 고쳐줘야죠
루트 노드가 없어져서 고장난 트리 고치는 방법
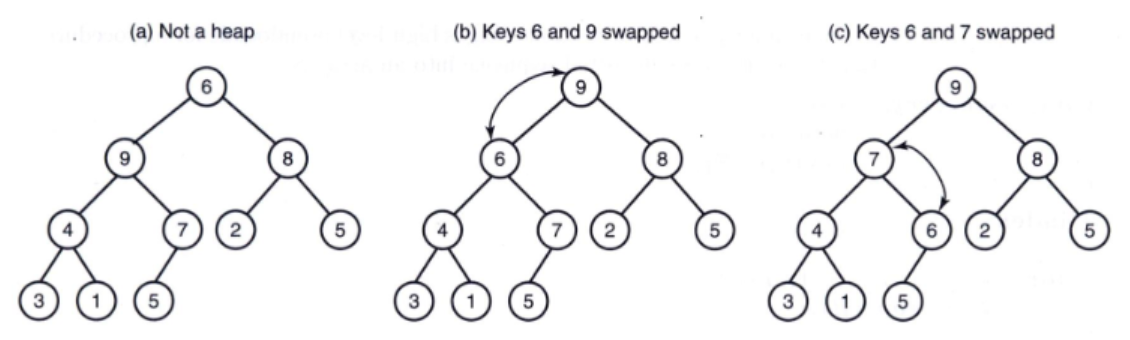
불순물 노드(아마 위에 올라간 녀석) 밑으로 내려주기
//root 노드를 맞는 위치에 넣어주기
void siftdown(heap& H) {
node parent, largerchild;
parent = root of H; //H의 부모? root?
largerchild = "parent's child containing larger key"; //자식 중에 더 큰 값을 갖고 있는 자식
while(key at parent is smaller than key at largerchild) //자식의 key 값이 부모보다 더 큰가?
exchange key at parent and key at largerchild; //서로 바꿔주기
parent = largerchild // 자식이 새로운 부모가 되어서 계속 진행
}
}
}heap 만들기
void makeheap(int n, heap& H) {
index i;
heap Hsub;
for(i = d - 1; i >= 0; i--) //밑에서부터 root까지 올라감
for(all subtree Hsub whose roots have depth i) //depth가 i인 자식노드들
siftdown(Hsub); //트리 정리해줌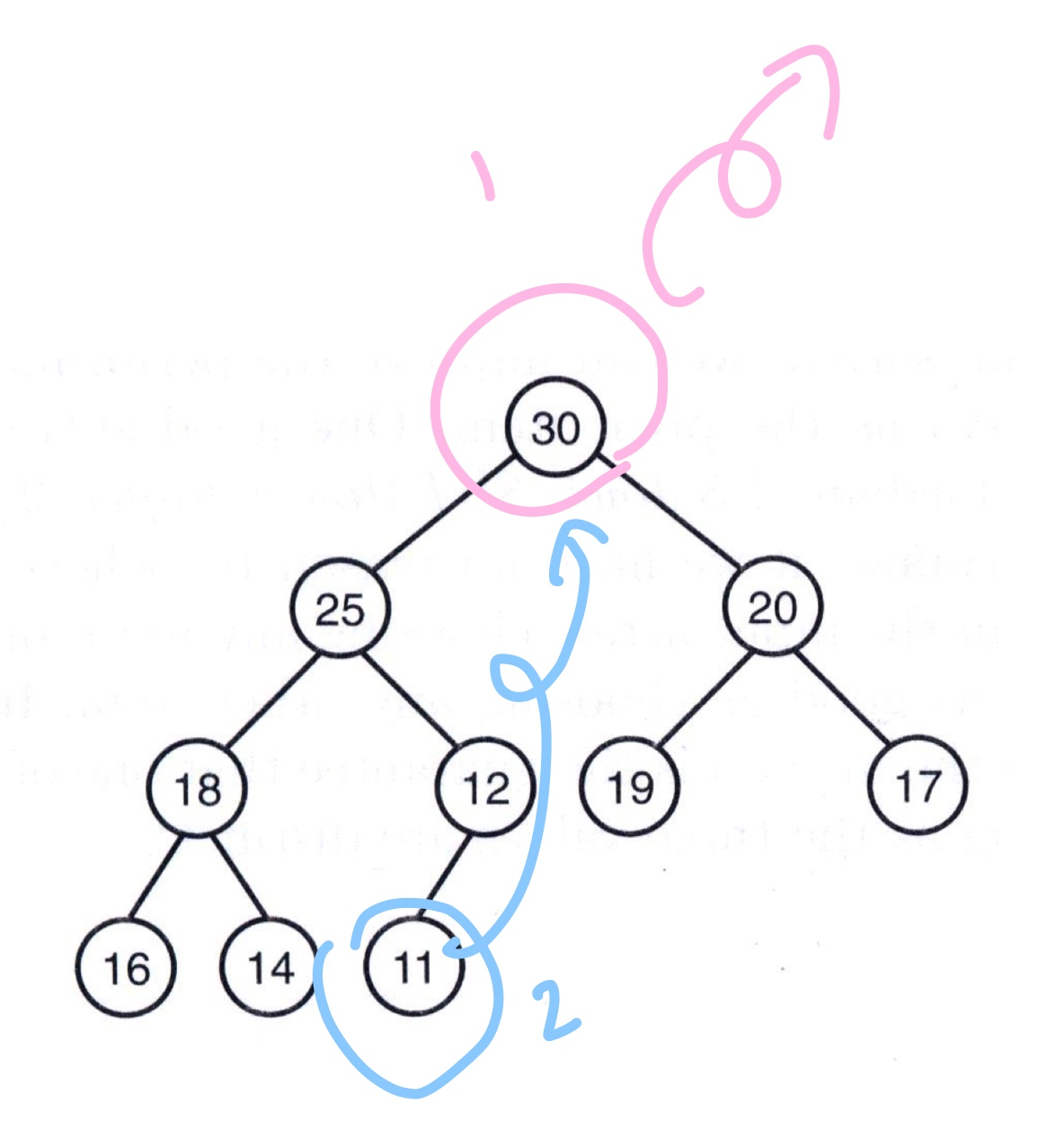
1. root노드의 값을 return해주고 가장 마지막 노드의 값을 root로 올려주기
2. heap 정렬이 깨졌으니 siftdown해주기
keytype root(heap& H) {
keytype keyout;
keyout = key a the root; //root의 key값?
move the key at the bottom node to the root; //마지막 노드를 root로 옮기기
delete the bottom node; //비어버린 마지막 노드 지우기
siftdown(H);//노드 재정렬
return keyout; //root값 return 해주기removekeys
void removekeys(int n, heap& H, keytype S[]) {
index i;
for(i = n; i >= 1; i--)
S[i] = root(H); //root node값 빼와서 올려주는 함수..
}heapsort
void heapsort(int n, heap H, keytype S[]) {
makeheap(n, H); //heap만들기
removekeys(n, H, S); //값 꺼내오기
}make heap의 worst case...

잘 모르겠어요 언젠가 수학공부 다시 하면 해볼게요,,
아무튼 heap이란?
바이너리 트리에 값을 넣고
바이너리 트리의 root값은 트리의 가장 큰 값이니까 그 값을 꺼내고
루트 자리에 가장 작은 값을 넣고 heap이 깨졌으니 다시 정렬하고(siftdown)
heapsort(makeheap, removekeys)
makeheap(siftdown)
removekeys(root)
root(루트 값 돌려주고 밑에 있는 값 가져오기, siftdown)
3개의 key를 정렬하는 경우
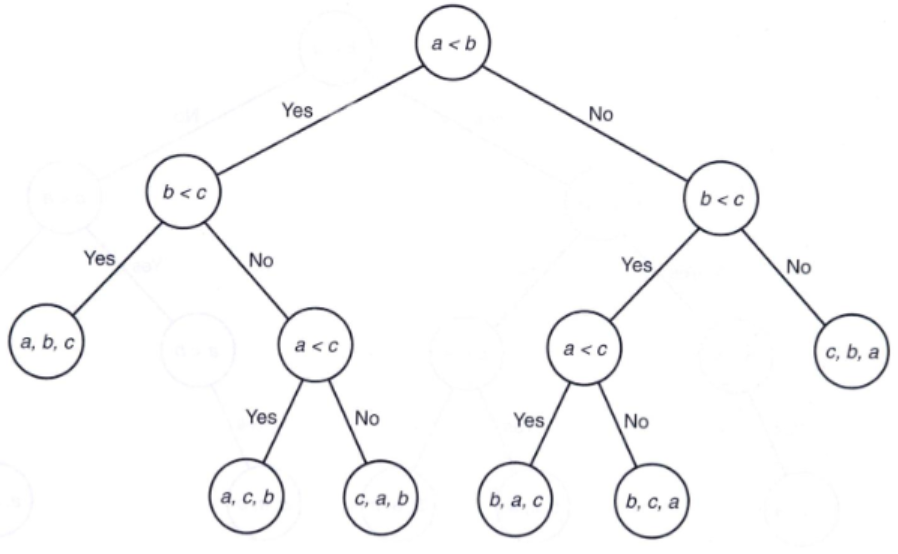
void exchangesort() {
index i, j;
for(i = 0; i < n; i++)
for(j = i; j < n; j++)
if(S[j] < S[i]) exchange
}아무튼 비교비교 한다..~