Monte Carlo Algorithm
- 확률적 알고리즘으로 확률적 분포에 따라 무작위로 결정된다.
In backtracking Algorithm
- backtracking 알고리즘의 효율성을 추정할 때 사용할 수 있다.
- state space tree의 동일한 level에서는 동일한 promising function을 사용
- 동일한 level의 node에는 동일한 수의 자식 노드가 있어야 함.
Monte Carlo Algorithm in 4 - queens problem
4-queens problem에서 monte carlo algorithm으로 backtracking algorithm의 효율성 측정하기
-> 실제 방문해야할 노드를 추정

1. i 번째 노드에서 n개 중에 3개정도를 조사하였을 때 한 개가 promising하다면 mi가 promising할 확률은 1/3 = mi
2. mi = 1/3ti
3. 그렇다면 이 트리에서 탐색해야하는 노드의 개수는 (state space tree size)
1+ t0 + m0 * t1 + m0 * m1 * t2 ... (mi <= ti)
// 1(start node) + t0(전체 노드가 해당 가능) + m0(유의미한 노드만 확인) *
t1(전체 노드의 개수만큼 확인이지만 부모노드는 확인할 수 없으니 -1) -> 1 + 4 + 4 * 3
N queens problem

4- queens problem과 동일한 방식
Sum of Subsets Problem(부분 집합 문제)
- w의 합이 W이 되는 부분집합
- 가중치 + n이 유망한가?

- w의 합이 W가 되는 set
Promising 하지 않은 경우
- weight + 다음 노드가 W보다 큰 경우
- weight + 다음 노드 전부가 W보다 작은 경우
- i는 젤 작은 경우?
Input
- 양의 정수 n개를 갖고 있는 wi ?
- 양의 정수 W



지금까지 계산한 w를 W와 비교
case1. weight가 W와 동일한 경우
-> return
case2. weight + 다음 노드 > W
-> 자식노드 하나만 비교했는데도 넘치기 때문에 더이상 진행 x
case3. weight + 다음 노드 전부 < W
-> 하위 노드 전부(total)를 더해도 W보다 작기 때문에 진행 x
Graph Coloring Problem
: 인접한 노드와 겹치지 않게 색을 칠할 수 있는 최소 개수 m
input
- 꼭짓점의 개수 n과 색의 수 m
- n개의 정점을 포함하는 무방향 그래프
- 두 모서리가 서로 교차하지 않는 그래프(planar graph)
idea : 색상의 지정된 정점 a의 인접한 정점은 a의 색상을 사용할 수 없다.(non-promising)
=> 사실 결과는 4개라고 나와있음!
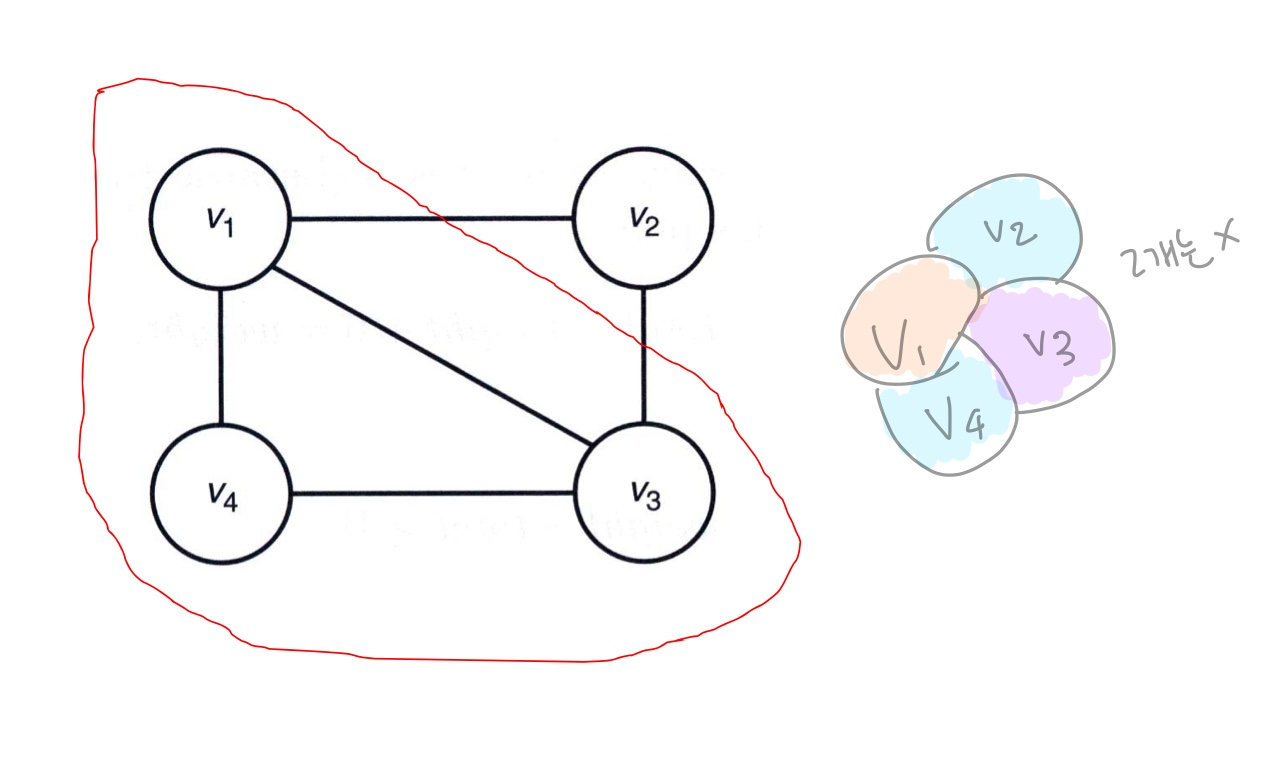
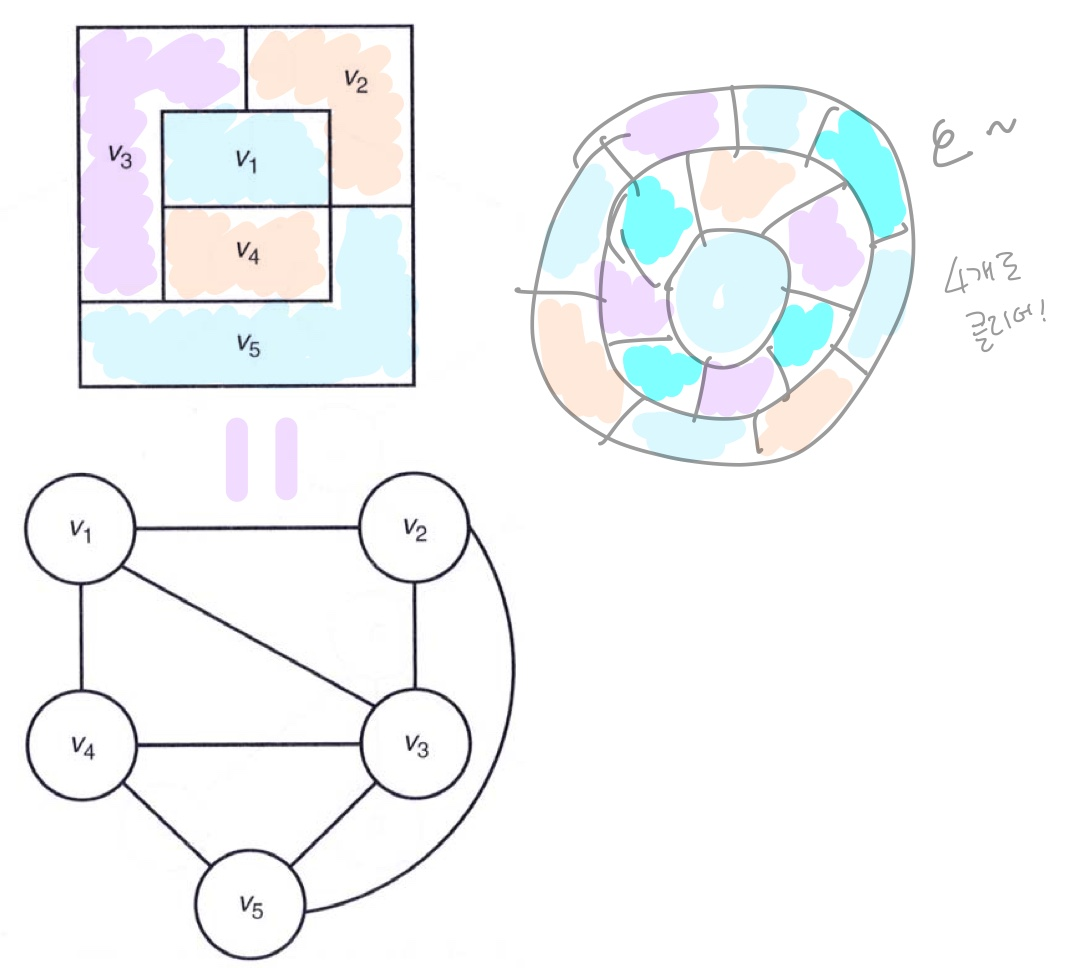
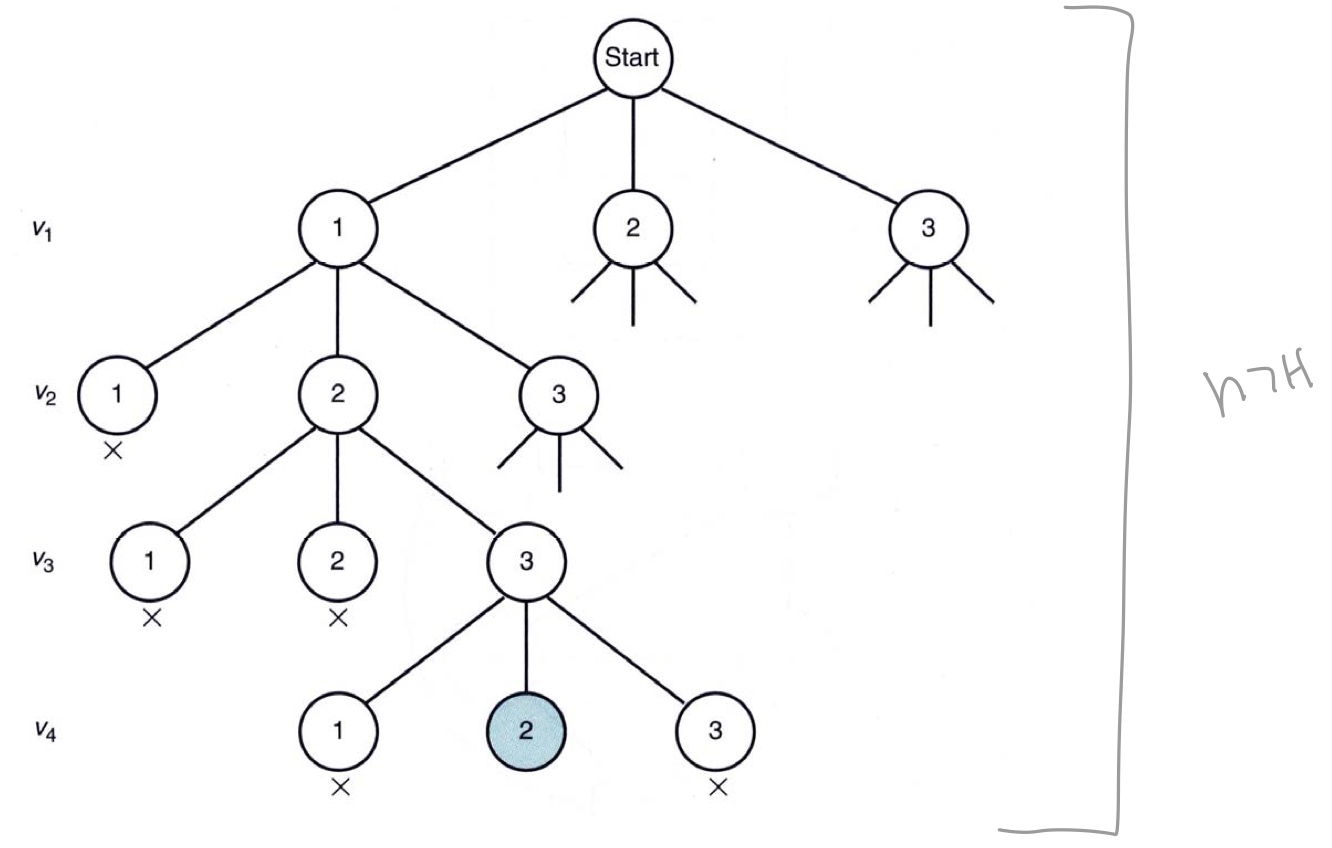
아무튼 n개의 노드의 색을 정해야하기 때문에 n번 확인해야한다.
The total number of nodes in a state space tree
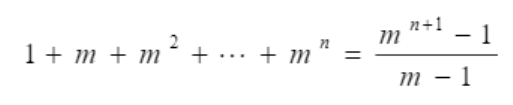
단계별 m개를 n번하는 어쩌구 저쩌구
Hamiltonian Circuits Problem
: 모든 경로 찾기
- 주어진 꼭짓점에서 출발해서 각 꼭짓점을 한 번씩 방문하고 시작점으로 되돌아옴.
input
- n개의 정점을 포함하는 무방향 그래프
- 시작점 vi
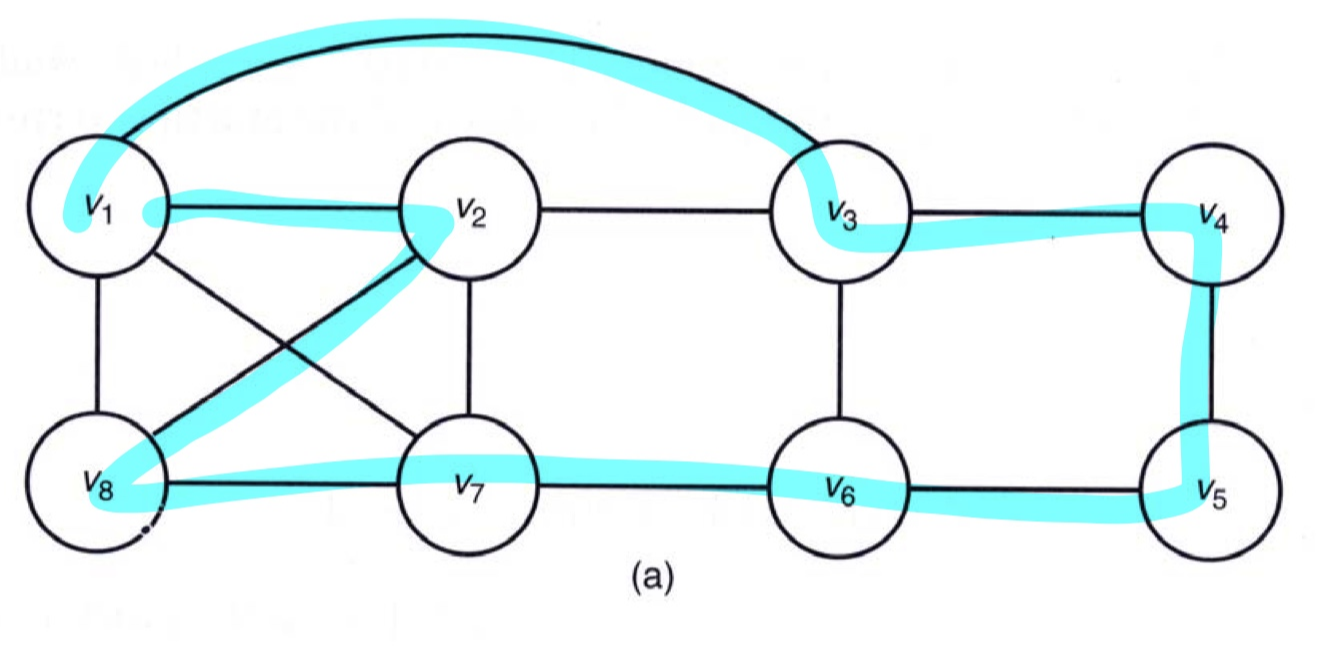
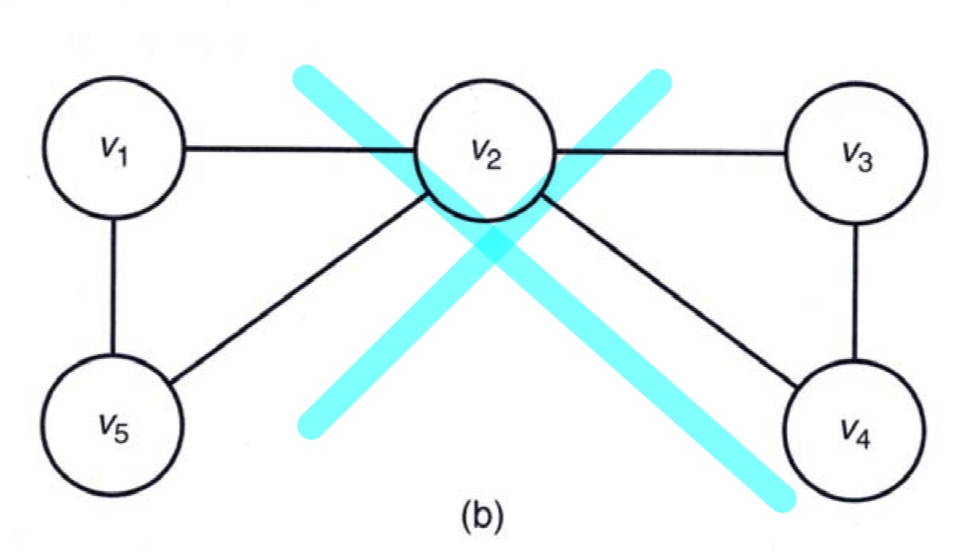
The total number of nodes in state space tree
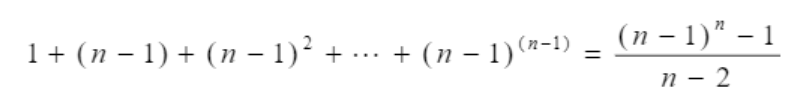
왜일까?
왜 1 + (n - 1) + 1 * (n - 1) * ( n - 2) * ... 이게 아닌걸까
아니 지났던 정점은 돌아갈 수 없는데 왜 계속 가능성을 열어놓죠?
아무튼 나중에 다시 한 번 살펴보는걸로..
'아무튼 공부중 > algorithm' 카테고리의 다른 글
| [알고리즘] The Traveling Salesperson Problem(외판원 문제) (0) | 2023.12.13 |
|---|---|
| [알고리즘] Branch and Bound Algorithm | 분기 한정법 (0) | 2023.12.11 |
| [알고리즘] Backtracking | n Queens Problem (0) | 2023.12.03 |
| [알고리즘] Chained Matrix Multiplication (연쇄 행렬 곱셈) (1) | 2023.10.24 |
| [알고리즘]Graph Theory | 그래프 이론 (1) | 2023.10.22 |