Big O (빅오)

정의 : 점근적 상한선
주어진 복잡도 함수 c×f(n)에 대해 음이 아닌 정수 n이 N보다 크고 양수인 정수 c가 존재한다면 O(f(n))은 g(n)보다 큰 함수들의 집합이다. => g(n) ≤c×f(n)
g(n)이 알고리즘에 대한 시간복잡도라면 결국 알고리즘의 시간복잡도의 최대값은 f(n)보다 클 수 없기 때문에 g(n)은 O(f(n))이라고 할 수 있다.
-> g(n)은 c×f(n)보다 느리게 실행될 수 없기 때문
∴ g(n)의 시간복잡도는O(f(n))이다.
Example

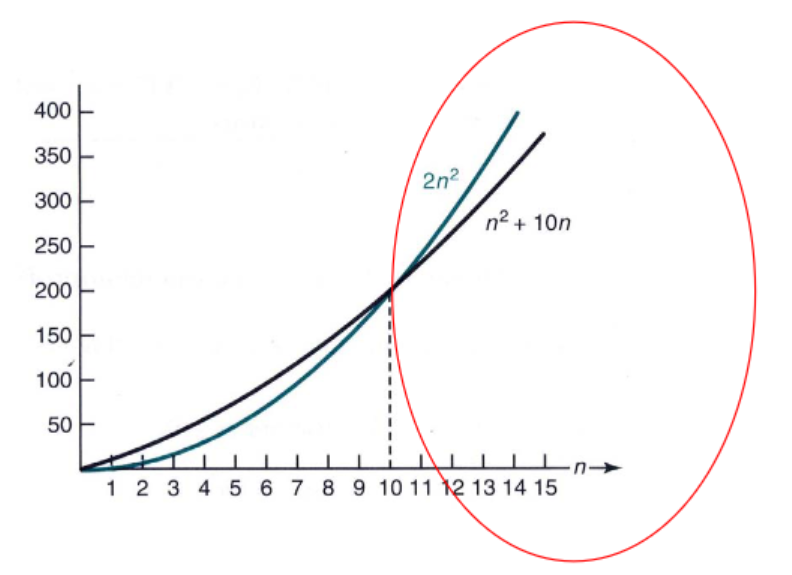
아무튼 이런 시간복잡도를 갖고 있는 알고리즘은 n^2의 속도로 빨라지게 되고
2n^2보다는 느릴 것이다.
결과적으로 n^2 +10n은 2n^2보다 작은 값을 갖게 된다.
Ω(오메가)

정의 : 점근적 하한선
주어진 복잡도 함수 f(n)에 대해 음이아닌 정수 n이 N보다 크고 양수인 정수 c가 존재한다면
Ω(f(n))은 g(n)보다 작은 함수들의 집합이다. => c×f(n) ≤ g(n)
g(n)이 알고리즘에 대한 시간복잡도라면 결국 알고리즘의 시간복잡도의 최소값은 f(n)보다 작을 수 때문에 g(n)은 Ω(f(n))이라고 할 수 있다.
-> c×f(n)은 g(n)보다 느리게 실행될 수 없기 때문
∴ g(n)의 시간복잡도는Ω(f(n))이다.
Example

take c = 1 and N = 0 => 0 == 0
뭐 아무튼..
Θ(세타)

정의 : Asymptotic Tight Bound // 점근적인 상한과 하한의 어딘가?
주어진 복잡도 함수 f(n)에 대해 음이 아닌 정수 n이 N보다 크고 양수인 정수 c와 d가 존재한다면 Θ(f(n))은 그러한 함수의 집합이다. => c×f(n) ≤g(n) ≤d×f(n)
주어진 복잡도 함수 f(n)에 대하여, Θ(f(n))은 모든 n > N에 대하여, 일부 양의 실수 상수 c와 d와 일부 음이 아닌 정수 N이 존재하는 복잡도 함수 g(n)의 집합이다.
c×f(n) ≤g(n) ≤d×f(n)
O(n^2), Ω(n^2), Θ(n^2)의 예시


Small o(스몰 오)
주어진 복잡도 함수 f(n)에 대해 음이아닌 정수 n이 N보다 크고 모든 정수인 실수 c가 존재한다면
o(f(n))은 g(n)보다 큰 함수들의 집합이다. => g(n) ≤c×f(n)
Big O vs Small o
Big O : some positive real constant c
Small o : every positive real constant c
∴g(n)이 o(f(n))이라면 g(n)은 f(n)보다 훨씬 낫다.
'아무튼 공부중 > algorithm' 카테고리의 다른 글
| [알고리즘]Quicksort (0) | 2023.10.20 |
|---|---|
| [알고리즘]The Master Theorem, Auxiliary Master Theorem (0) | 2023.10.19 |
| [알고리즘] Binary Search, Mergesort(DIvide and Conquer) (1) | 2023.10.19 |
| [알고리즘] Analysis of Algorithm (0) | 2023.09.13 |
| [알고리즘] 순차 탐색, 이진 탐색, 피보나치 수열 (0) | 2023.09.13 |