Graph Theory
- 그래프는 G = (V, E)의 두 요소로 구성된다.
- vertex : 정점
- E : 간선들의 집합 | 간선들은 2개의 endpoint를 가진다.
- directed graph(digraph) : 방향성이 있는 그래프
- weighted graph(weights) : 값이 있는 그래프
- path : digraph에서 정점에서 목적지로 가는 방법(정점들을 담고 있는?)
- cycle : path가 돌아서 시작점으로 돌아옴
ㄴcycle인 그래프를 cyclic, 그렇지 않으면 acyclic
- simple : 같은 정점을 다시 돌아오지 않는 경우
- length : weighted graph에서 weights들의 합
Example : A weighted, directed graph


Floyd's algorithm for Shortest Paths Problem
- Problem : 가중치 그래프의 각 정점에서 다른 정점으로의 최단 경로 계산
- Input : 가중치 그래프(weight digraph), 꼭짓점의 갯수, 정점 i부터 정점 j까지의 weight가 있는 W[i][j]
- Output : 행과 열이 1부터 n까지 값이 정해진 2차원 배열 D, 정점 i부터 정점 j까지의 최단경로가 담겨있는 D[i][j]
Brute-force algorithm for Shortest Paths
- 전략 : 모든 경로를 찾아서 전부 계산한 후 최단 거리를 찾는다.
- 분석 : vi에서 vj까지의 총 경로의 수는 (n-2)!
-> 팩토리얼값은 지수보다 더 나쁘다
=> 기각
Dynamic Programming Strategy for Shortest Paths

갈 수 있는 경우에 값을 넣어주고 갈 수 없는 경우에 무한을 넣어준다.
자기 자신까지 가는 경우는 0

k번 경유했을 때 Vi에서 Vj까지 가는 최단 경로 값 = D(k)[i][j]

새로운 경로를 찾을 때 더 적은 값을 골라준다.

Floyd's algorithm 1
//Floyd's algorithm 1
void floyd(int n, const number W[][], number D[][]) {
int i, j, k;
D = W; //D(0)은 W < 아무것도 없는 그래프에 갖고 있는 값으로 초기 설정
for(k = 1; k <= n; k++) //중간에 나누는 값
for(i = 1; i <= n; i++) //행
for(j = 1; j <= n; j++) //열
D[i][j] = minimum(D[i][j], D[i][k] + D[k][j]);
//바로 가는 것과 경유 중 더 적은 값을 골라줌
}Every Case Time Complexity
T(n) = n x n x n ∈ Θ (n^3)
Floyd's algorithm 2
- Problem : 최소값은 알려줬는데 경로는 안알려줌
- Additional outputs : 1부터 n까지 가는 방법이 담긴 배열 P

vi에서 vj로 가는 가장 짧은 경로에 있는 중간 정점의 가장 빠른 인덱스
(최소 하나 이상의 중간 정점이 존재하는 경우) vs 경유지가 없는 경우
//Floyd's algorithm2
void floyd2(int n, const number W[][], number D[][], index P[][]) {//P에 경로 저장
index i, j, k;
for(i = 1; i <= n; i++){ //P[][]초기화
for(j = 1; j <= n; j++){
P[i][j] = 0;
D = W; //사용할 경로 초기값 설정
for(k = 1; k <= n; k++) //중간에 나누는 값
for(i = 1; i <= n; i++) //행
for(j = 1; j <= n; j++) //열
if(D[i][k] + D[k][j] < D[i][j]) { //경유하는 노선이 더 빠르다면
P[i][j] = k; //i에서 j로 갈 때 k를 지남을 표시
D[i][j] = minimum(D[i][j], D[i][k] + D[k][j]);
}
}Print Shortest Path
//Print Shortest Path
void path(index q, r) {
if(p[q][r] != 0) {
path(q, P[q][r]);
cout << "v" << P[q][r];
path(P[q][r], r);
}
}The Principle of Optimality(최적성의 원리)
음
최적화를 했으면 그거에 맞는 코드를 써야한다..~
v5에서 v3까지 가는 방법을 최적화해서 v4를 들린다면
v5에서 v4까지 가는 방법도 최적화 된 방법을 써야한다..
라는걸까요?
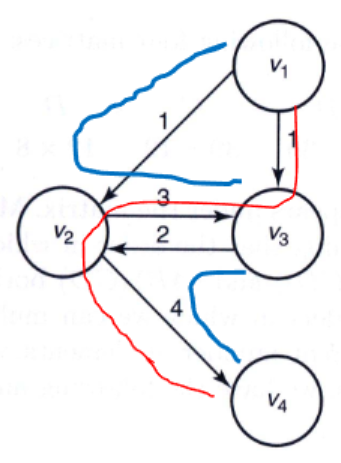
예를 들어 가장 먼 방법을 사용했다고 해서 v1-> v2->v3->v2->v4로 진행하게 되면 v2를 2번 지나게 되어서 simple하지 않게 되는 것 처럼..
유의하자..
어렵군요..
'아무튼 공부중 > algorithm' 카테고리의 다른 글
| [알고리즘] Backtracking | n Queens Problem (0) | 2023.12.03 |
|---|---|
| [알고리즘] Chained Matrix Multiplication (연쇄 행렬 곱셈) (1) | 2023.10.24 |
| [알고리즘]The Binamial Conefficient with Pascal's Triangle | 파스칼의 삼각형을 이용한 이항계수 알고리즘 (1) | 2023.10.21 |
| [알고리즘]Matrix Multiplication with Strassen's Algorithm (1) | 2023.10.21 |
| [알고리즘]Quicksort (0) | 2023.10.20 |