Dynamic Programming (동적 계획법)
Bottom up 방식으로 작은 값 부터 구하기 시작하여 결과를 도출한다.
작은 값부터 시작하는건 DIvide and Conquer랑 비슷하시지만 밑에서부터 시작한다는 점에서 차이점이 있다.
Bottom up 방식이기 때문에 한 번 계산한 결과를 다시 계산할 필요 없이 저장된 결과를 불러서 사용한다.
The Binamial Conefficient(이항계수)
조합 nCr
n개에서 r개를 순서 상관없이 골라내는 경우의 수


전체 경우의 수 n! 에서 필요없는 나머지 경우의 수 (n-1)!을 나누고 순서가 상관 없기 때문에 뽑은 갯수 k!만큼 또 나눠주기~
Pascal's Triangle
대각선 위에 있는? 값들의 합은 아래에 있는 값이 된다!
조합을 사용해서 첫번째 식으로 나타낼 수 있다.



Binomial Coefficient using Divide and Conquer
- Problem : nCk
- Input : 음이아닌 정수 n, k (k <= n)
- Output : nCk가 계산된 값?
//Binomial Coefficient using DAC
void bin(int n, int k) {
if(k == 0 || n == k)
return 1;
else
return bin(n-1, k-1) + bin(n-1, k);
}Time Complexity for Binomial Coefficient using Divide and Conquer
- Basic operation : 계산할 항의 갯수?
- Input size : n k
- Proof by Induction

이렇게 가정한 뒤에 n = n + 1을 계산해보자~
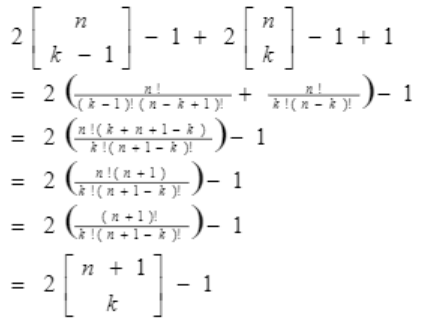
< 그냥 계산을 하면 뭔가 결과가 나옴..
시간복잡도는 앞에꺼 뒤에꺼 그리고 둘을 더해서 이런식으로 나옴.. 아마두
T((n+1) C k) = T(n C (k-1)) + T(n C k) + 1
< 조합의 형태로 시간복잡도가 나오면 값이 너무 커서 좋지 않음.
Dynamic Programming for Binomial Coefficient

이항계수를 동적프로그램으로 계산하기(파스칼의 삼각형)
bottom up 방식으로 전부 계산해준다.
Binomial Coefficient using Dynamic Programming
- Problem : n C k
- Input : 음이아닌 정수 n, k ( k <= n)
- Output : nCk가 계산된 값?

//Binomial Coefficient using Dynamic Programming
void bin2(int n, int k) {
index i, j;
int B[0...n], [0...k];
for(i = 0; i <= n; i++) //전체 사이즈
for(j = 0; j <= min(i,k); j++) //삼각형의 대각선 방향..1이 나오는 경우까지 돌림
if(j == 0 || j == i) B[i][j] = 1; //nC0이거나 nCn인 경우 < 초기값
else B[i][j] = B[i - 1][j - 1] + B[i - 1][j]; //값 넣어주기
return B[n][k];
}Time Complexity for Binomial Coefficient using Dynamic Programming
- Basic operation : 계산할 항의 갯수?
- Input size : n k
전부 더해줌..
i = k + 1의 경우는 k + 2가 아니라 k + 1임!
-> i가 k보다 크고 k는 상수니까 k + 2는 의미가 없다. ->그래서 n - k + 1번의 k + 1 존재함.

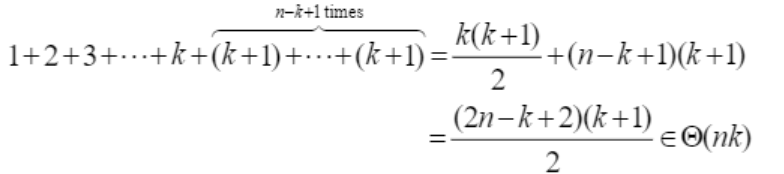
Divide and Conquer방식의 시간복잡도는

Dynamic Programming(파스칼의 삼각형)방식의 시간복잡도는

∴ Dynamic Programming방식이 더 좋다!
'아무튼 공부중 > algorithm' 카테고리의 다른 글
| [알고리즘] Chained Matrix Multiplication (연쇄 행렬 곱셈) (1) | 2023.10.24 |
|---|---|
| [알고리즘]Graph Theory | 그래프 이론 (1) | 2023.10.22 |
| [알고리즘]Matrix Multiplication with Strassen's Algorithm (1) | 2023.10.21 |
| [알고리즘]Quicksort (0) | 2023.10.20 |
| [알고리즘]The Master Theorem, Auxiliary Master Theorem (0) | 2023.10.19 |