Matrix Multiplication
: 행렬의 곱은 어떻게 계산 할까
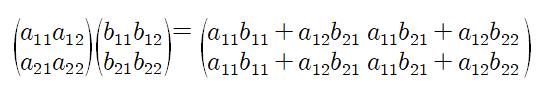
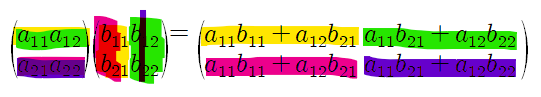
//Matrix Multiplication
//Standard Algorithm
void matrixmult(int n, const number A[][], const number B[][], number C[][]) {
index i, j, k;
for (i = 1; i <= n; i++)
for(j = 1; j <= n; j++) {
C[i][j] = 0;
for(k = 1; k <= n; k++)
C[i][j] = C[i][j] + A[i][k] * B[k][j]; //왜 C[i][j]를 초기화해서 쓰는걸까?
}
}T(n) = n x n x n = n^3 ∈ Θ(n^3) //for문을 3번 돌렸기 때문!
Matrix Multiplication : Strassen's Method
strassen씨가 만든 행렬 곱 계산 공식!
왼쪽은 2 x 2 행렬이고 오른쪽은 n x n 행렬에 대한 공식인데
일반적인 행렬 곱을 진행할 때 곱셈을 처리하는 것 보다 덧셈을 처리하는게 시간복잡도가 더 좋으니 덧셈을 사용하여 계산을 할 수 있는게 strassen의 알고리즘이다.


Strassen's Algorithm
- Problem : n은 2의 거듭제곱인 nxn 행렬 두 개의 곱은?
- Input : 2의 거듭제곱인 n과 n x n 행렬 A와 B
- Output : A와 B를 곱한 행렬 C
//Strassen's Algorithm
void strassen(int n, n*n_martix A, n*n_martix B, n*n_matrix& C) {
if(n <= threshold)
compute C = A * B; //계산 할 수 있으면 계산하기
else { //아니면 행렬을 잘게 쪼개서 strassen의 방법으로 계산하기
partition A into four submatrices A11, A12, A21, A22; //쪼개기
partition B into four submatrices B11, B12, B21, B22; //쪼개기
Compute C = A * B using strassen's method; //계산하기
//example recursive call : strassen(n/2, A11+A12, B11+B22, M1)
//threshold의 값까지 내려가서 계산하며 처리하며 올라오기!sudo code 이해하기

A와 B를 끊임없이 쪼갬
-> 결과적으로 DIvide and Conquer이 되는 것!!
strassen(행렬 A, 행렬 B, 새로운 행렬 C) {
if(일반적인 계산이 더 이득일 것 같은 경우)
일반적으로 C = A * B를 계산해줌
else { //계산이 복잡한 경우
행렬 A를 4개의 행렬로 나눠줌
행렬 B를 4개의 행렬로 나눠줌
step1. M1부터 M7까지의 경우를 호출함
ex1. strassen(n/2, (A11+A22), (B11+B22), M1)
//M1 = (A11+A22)x(B11+B22) 이므로 M1이라는 행렬에 (A11+A22)와 (B11+B22)의 곱 행렬 값을 넣어줌
ex2. strassen(n/2, (A21+A22), B11, M2)
//M2 = (A21+A22) x B11이므로 M2라는 행렬에 (A21+A22)와 B11의 곱 행렬을 넣어줌
...
M7까지 반복
-> 이 과정에서 계산이 가능할 때까지 재귀가 발생함
ㄴ if(일반적인 계산이 더 이득일 것 같은 경우)에서 계산을 진행하기 때문
step2. M1부터 M7까지의 경우가 계산 된 경우 산술계산을 해줌Every Case Time Complexity Analysis of Number of Multiplications (Strassen)

-> input 값과 상관없이 크기 n의 행렬은 같은 시간복잡도를 갖기 때문에 Every Case Time Complexity
- Basic operations : one elemetary multiplcation
- Input size : 행렬의 크기?
T(n)은 M1부터 M7까지 7개의 T(n/2)를 호출하기 때문에
아무튼 계산하면
T(n) ∈ Θ (n^2.81)
Every Case Time Complexity Analysis of Number of Additions/Subtractions (Strassen)

M1부터 M7까지 7개의 T(n/2)를 호출하고(7T(n/2)) 총 18의 산술연산(n * n이기 때문에 제곱의 경우의 수 만큼 진행함 => 18(n/2)^2))을 계산하기 때문에
T(n) = 7T(n/2) + 18(n/2)^2 = Θ (n^2.81)
결론?

아무튼 이렇게 시간복잡도도 열심히 계산해 본 결과
standard algorithm보다 strassen's algorithm이 더 좋다는 것을 알 수 있다~
'아무튼 공부중 > algorithm' 카테고리의 다른 글
| [알고리즘]Graph Theory | 그래프 이론 (1) | 2023.10.22 |
|---|---|
| [알고리즘]The Binamial Conefficient with Pascal's Triangle | 파스칼의 삼각형을 이용한 이항계수 알고리즘 (1) | 2023.10.21 |
| [알고리즘]Quicksort (0) | 2023.10.20 |
| [알고리즘]The Master Theorem, Auxiliary Master Theorem (0) | 2023.10.19 |
| [알고리즘] Binary Search, Mergesort(DIvide and Conquer) (1) | 2023.10.19 |